Tension hachée et pertes par effet Joule (4)

Nous terminons la série d’articles par les équations du courant dans le moteur ainsi que le calcul des pertes par effet Joule pour la conduction continue.

On rappelle les grandeurs manipulées :

• U₀ — la tension d’alimentation du moteur ;
• V_D — la tension de seuil de la diode roue libre ;
• E — la force contre-électromotrice ;
• L — l’inductance du moteur ;
• R — la résistance du moteur ;
• T — la période de la PWM ;
• h — le rapport cyclique de la PWM ;

h est exprimé relativement à la période T.

On rappelle la forme générale de la tension et du courant en conduction continue :

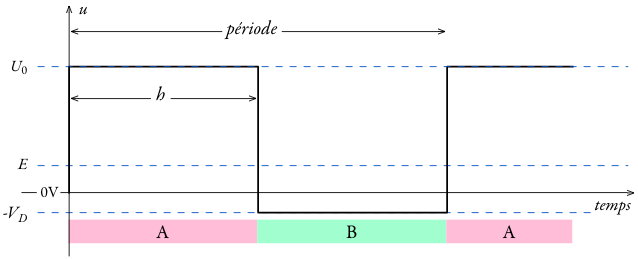
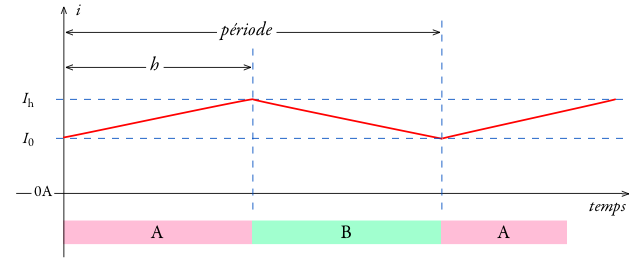
Pour ce qui suit, on pose :

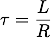
Les formules et les équations

Le courant moyen dans le moteur :

Le courant minimum dans le moteur :

Le courant maximum dans le moteur :

La puissance moyenne consommée par le moteur :

La puissance moyenne utile (transformée en puissance mécanique) :

Les pertes par effet Joule dans la diode roue libre :

Les pertes par effet Joule dans le moteur :

Le courant efficace :

Plusieurs remarques :

• si on trouve I₀ négatif, c’est que l’hypothèse de conduction continue n’est pas vérifiée : la conduction est en fait discontinue ;
• comme pour la conduction discontinue, calculer directement l’expression du courant efficace est très compliqué : on préfère déduire les pertes par effet Joule à partir des autres puissances.

Détail des calculs en conduction continue

Les équations différentielles du courant dans le moteur sont :

• pour 0 ≤ t ≤ hT

avec i(0) = 0 et i(hT) = I_h

• pour hT ≤ t ≤ T

avec i(hT) = I_h et i(T) = I₀

Nous pouvons calculer le courant moyen I_moy dans le moteur sans avoir calculé ni I₀ ni I_h.

Nous calculons successivement I_moy0 et I_moy1. Nous écrivons l’équation différentielle du courant entre 0 et hT sous la forme :

Ainsi :

De même, nous écrivons l’équation différentielle du courant entre hT et T sous la forme :

Ainsi :

de 41 et 44 :

Pour calculer I₀ et I_h, nous avons besoin de résoudre les équations différentielles :
Entre 0 et hT :

Entre hTet T :

Puis on exprime que le courant ne présente pas de discontinuité en t = hT :

et en t = T :

Il faut donc résoudre en I₀ et I_h le système où on a posé

On obtient :

et :

Nous allons maintenant évaluer les valeurs moyennes des différentes puissances qui entrent en jeu :

P_c valeur moyenne de la puissance totale consommée ;
P_u valeur moyenne de la puissance utile, c’est à dire la puissance électrique transformée en puissance mécanique ;
P_Jm valeur moyenne des pertes Joules du moteur ;
P_Jd valeur moyenne des pertes Joules dans la diode roue libre.

Ces valeurs sont liées par la relation :

Il est difficile d’évaluer directement P_Jm, sa valeur sera obtenue à partir des valeurs des autres puissances. La valeur moyenne de la puissance totale consommée est égale à la puissance moyenne fournie par la source :

Or, i_S est égal à i entre 0 et hT et est nul entre hT et T :

Nous avons déjà calculé cette intégrale en 41 ; d’où :

La puissance utile instantanée est égale au produit de la fcem du moteur par valeur instantanée du courant i dans le moteur ; comme la fcem est constante, sa valeur moyenne est donnée par :

L’expression des pertes Joules dans la diode (le signe moins apparaît car u et i_d ont même orientation) :

Le courant dans la diode est nul entre 0 et ht et vaut i entre hT et T ; dans cet intervalle, la chute de tension directe dans la diode est considérée constante et égale à V_D.
Donc u=-V_D.

Cette intégrale a déjà été calculée en (44), d’où :